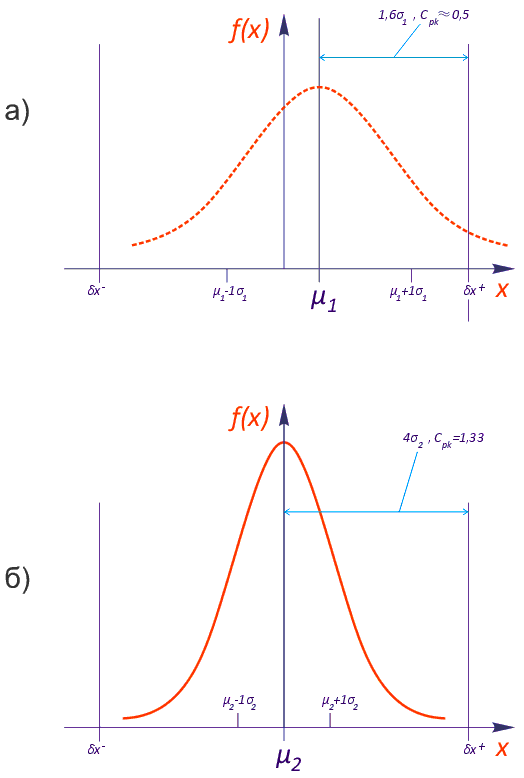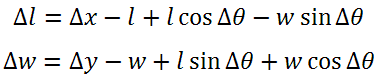|
|
Скоро!Событий нет.
|
20 марта 2000
Часть I. Показатели точности установочного оборудованияОглавление:
Точность и ее роль в сборочном процессе SMTКачество конечного изделия во многом зависит от правильного выполнения операции установки компонентов на печатную плату. Как известно, компоненты, монтируемые на поверхность печатных плат, при оплавлении паяльной пасты под действием сил поверхностного натяжения стремятся занять правильное положение, что явилось одним из аргументов в пользу технологии поверхностного монтажа для серийного и массового производства, где требуется высокая степень автоматизации. Однако при монтаже аппаратуры повышенной надежности, такой как, например, военная, медицинская, бортовая электроника, такой трудно контролируемый процесс, как самовыравнивание компонентов, не должен быть определяющим в достижении заданного уровня качества изготавливаемой аппаратуры. Кроме того, с переходом на бессвинцовую технологию стали применяться припои, которые обладают свойством выравнивания компонентов в значительно меньшей степени, чем традиционные оловянно-свинцовые сплавы. И, наконец, продолжающаяся микроминиатюризация изделий приводит к необходимости применения компонентов настолько малых размеров и с таким частым расположением выводов, что смещение компонента на несколько десятков микрометров может приводить к браку. Поэтому одним из первых параметров, на которые обращают внимания современные производители электроники при выборе автомата установки компонентов для поверхностного монтажа, является точность. Под точностью производства понимают степень соответствия изготовленного изделия заданным размерам, форме, механическим, физическим и иным характеристикам, вытекающим из назначения этого изделия. Точность выполнения операции отличается от точности всего процесса. Например, в приложении к SMT, благодаря самовыравниванию компонентов допустимая точность установки может быть ниже заданной точности процесса сборки. Точность сборочной операции характеризуется отклонением положения установленных изделий, от заданных (номинальных) положений, называемым погрешностью установки. Диапазон, образованный максимальными отклонениями, не приводящими к браку конечного изделия, называется полем допуска (англ. tolerance). Под точностью оборудования (в частности, автоматов установки компонентов), вообще говоря, понимают практическую способность этого оборудования обеспечить заданную точность выполнения операции в определенных производственных условиях и при достаточно малом влиянии факторов, не определяющихся этим оборудованием. Иными словами, точность автомата не учитывает факторы, не связанные с самим автоматом, например, точность изготовления печатной платы и электронных компонентов (ЭК). Максимальное отклонение и вероятностный допускРеальное положение любого компонента всегда несколько отличается от номинального. При этом смещение компонента может приводить к браку (если, например, это вызывает короткое замыкание с соседним компонентом или отсутствие контакта с площадкой на плате), а может не сказываться на качестве изделия. В идеале, оборудование должно обеспечивать установку всех компонентов со смещением в пределах поля допуска, т.е. отклонение положения компонента от номинального не должно превышать некоторого максимального значения. На практике всегда существует вероятность, что компонент будет установлен вне поля допуска, что приводит к появлению брака. Частично этот брак может быть устранен средствами контроля и производственных испытаний, однако данные меры повышают стоимость производства, и, кроме того, на этапе контроля также существует вероятность пропуска дефекта. Поскольку обычно электронные устройства содержат достаточно большое число компонентов, а автоматическая установка применяется преимущественно в серийном и массовом производстве, то вероятность установки компонента вне поля допуска должна быть достаточно малой. С другой стороны, слишком жесткие требования к вероятности попадания в поле допуска приводят к необоснованному удорожанию оборудования и неадекватным мерам по обеспечению качества. Поэтому при разработке системы качества производства в зависимости от требований к конечному изделию и планируемых мер по контролю и устранению возникающего брака всегда принимают в расчет вероятностный допуск, который задается при определенной вероятности установки компонента со смещением не более заданного. Как известно, если на некоторый процесс оказывает влияние большое число независимых равноправных случайных факторов, распределенных равномерно, то сам процесс подчиняется закону распределения Гаусса, или нормальному закону распределения:
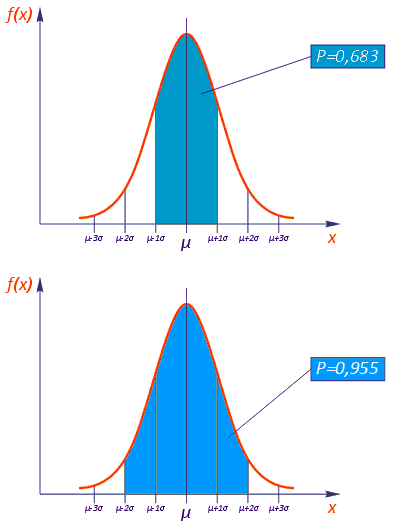
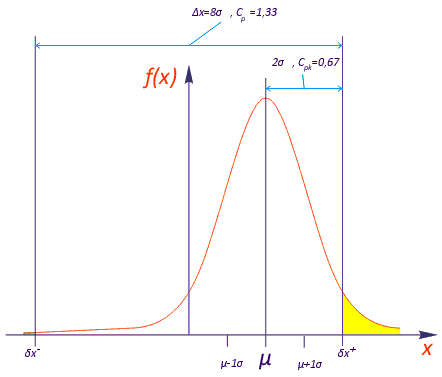
В данном случае x – смещение компонента по каждой отдельно взятой оси X или Y, либо отклонение по углу поворота θ вокруг оси Z. Вероятность попадания случайной величины x в заданный диапазон (–δx, +δx) равна интегралу f(x) по данному диапазону (рис. 1):
Эта вероятность, как несложно заметить, определена двумя величинами: математическим ожиданием μ и среднеквадратичным отклонением σ. Поскольку вероятность смещения компонента однозначно определяется двумя параметрами µ и σ, вместо вероятности установки компонента в заданное поле допуска можно указать эти два параметра. Например, параметры µ = 0 и σ = 0,05 мм означают, что вероятность попадания величины в область с отклонением не более ±0,05 мм составляет примерно 0,683, т.е. 683 компонента из тысячи будут установлены со смещением не более 0,05 мм в обе стороны по одной из осей (см. рис. 1).
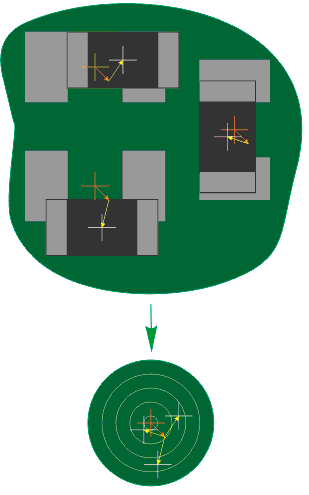
Рис. 1. Функция плотности вероятности для случайной величины, распределенной по нормальному закону Систематическая и случайная погрешностиПогрешность установки, как и любая погрешность, складывается из систематической и случайной погрешности. Систематическая составляющая погрешности выражается в смещении положения установленного компонента от номинального на постоянную величину. Т.е. под влиянием систематической погрешности все компоненты будут смещены одинаково. К систематическим погрешностям следует отнести те из них, которые связаны с точностью изготовления, сборки и наладки данного конкретного автомата – деталей его сборочных головок, приводов, устройства фиксации платы, значений настроечных параметров и пр. Отклонение этих величин от номинальных значений может вызвать неточное позиционирование сборочных головок, смещение и/или перекос печатной платы, смещение начала системы координат автомата и т.д. Случайная составляющая выражается в смещении каждого отдельного компонента на различную величину. Случайные ошибки возникают вследствие наличия погрешностей изготовления сборочных компонентов – ЭК и ПП, влияния окружающей среды – прежде всего, температуры и освещенности, питающих напряжений и создаваемого вакуума, точности алгоритмов распознавания образов ЭК и реперных знаков на ПП, вносящих коррекцию в положение захваченного сборочной головкой ЭК и зафиксированной платы, человеческого фактора – навыков и действий оператора и т.д.
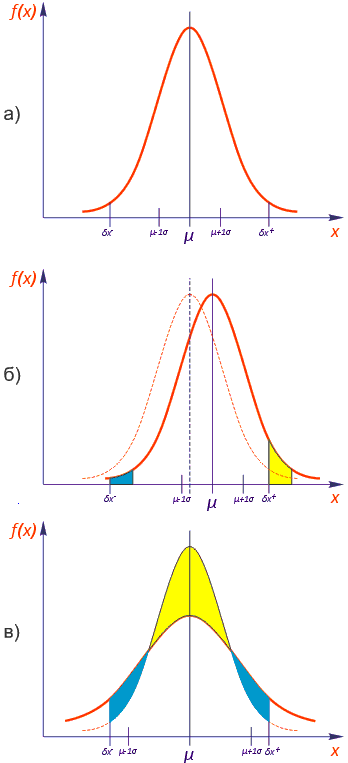
Рис. 2. Случайная и систематическая погрешности. Еще раз подчеркнем, что как систематические, так и случайные погрешности могут быть вызваны, с одной стороны, особенностями автомата, с другой – воздействующими факторами, не относящимися к самому автомату. Далее мы будем говорить только о точности оборудования, поскольку прочие факторы являются объектом системы качества предприятия, что выходит за рамки данной статьи. Иными словами, в дальнейших рассуждениях мы будем считать, что воздействия факторов, не определяющихся оборудованием, сведено к минимуму. На практике большого значения не имеет, какие именно факторы вызывают систематическую погрешность автомата. Важно, что их совокупное действие приводит к постоянному смещению. Чаще всего это смещение может быть скомпенсировано. В бо́льшую часть оборудования для поверхностного монтажа заложена возможность проведения калибровки, с помощью которой систематическую погрешность можно практически полностью устранить. Для случайных составляющих проведение такой процедуры, как элемента обслуживания оборудования, не представляется возможным. Математически совокупное действие факторов, вызывающих систематическую погрешность, выражается в отклонении величины математического ожидания µ от нуля. Случайная составляющая погрешности находит отражение в величине среднеквадратичного отклонения σ: чем больше σ, тем больше разброс положений компонентов вокруг точки с постоянным смещением µ. Изменение значения µ (систематическая погрешность) приводит к смещению графика нормального распределения вдоль оси абсцисс, увеличение σ вызывает «растягивание» графика, при этом уменьшается его максимальное значение, поскольку общая площадь под графиком на интервале (– ∞;+ ∞) должна оставаться равной единице.
Рис. 3. Влияние µ и σ на вероятность попадания в диапазон. При увеличении µ правая (желтая) фигура (см. рис. 3б) под графиком оказывается за пределами поля допуска, а левая фигура (голубого цвета) смещается в поле допуска. Но поскольку площадь левой фигуры всегда меньше правой, то суммарная площадь под графиком в поле допуска оказывается меньше, что соответствует меньшей вероятности правильной установки. При увеличении σ также уменьшается площадь под графиком в поле допуска, т.е. меньшее число компонентов оказывается установленными без брака. PPM и число сигмРанее мы привели пример: при значении параметров µ = 0 и σ = 0,05 мм 683 компонента из тысячи попадут в поле допуска ±0,05 мм. На практике данная вероятность 0,683 очень мала: число компонентов на одной плате может составлять несколько сотен, и в этом случае почти наверняка каждая плата окажется бракованной. Реальная вероятность должна быть на порядок выше. Численное выражение вероятности «правильной» установки будет иметь несколько девяток после запятой. С такими числами работать неудобно, поэтому на практике для определения вероятности попадания/непопадания компонента в поле допуска применяется показатель, равный среднему числу выходов за пределы поля допуска на миллион устанавливаемых компонентов, – ppm (parts per million). Итак, в указанном примере для поля допуска ±0,05 мм ppm = 317 тыс. Если с помощью данного автомата (с параметрами µ = 0 и σ = 0,05 мм) требуется достичь более реального значения ppm, нужно расширять поле допуска (т.е. отказаться от компонентов малого размера и малого шага выводов). Например, значению ppm = 2700 будет соответствовать поле допуска Δ = ±0,15 мм. Если же необходимо достичь такого значения ppm при сохранении поля допуска Δ = ±0,05 мм, то необходимо выбрать автомат, случайная составляющая погрешности которого в три раза меньше (т.е. σ ≈ 0,017 мм). Показатель ppm связан с вероятностью установки компонента в поле допуска соотношением ppm =1 000 000 (1 – P (–δx < x < +δx)). Как мы уже отмечали, чем больше значение σ, тем меньше вероятность попадания компонента в поле допуска. Если поле допуска расширить, то очевидно соответствующая вероятность увеличится. При µ = 0 выражение для вероятности попадания в поле допуска (–δx, +δx) приобретает вид:
Очевидно, данная вероятность зависит только от отношения δx/σ, то есть от числа сигм, укладывающихся в половине поля допуска. Итак, значение ppm связано с отношением половины ширины поля допуска к значению σ. Значение ppm = 317 тыс при Δ / 2σ = 1, ppm = 2700 при Δ / 2σ = 3. Поскольку на практике удобно работать с величиной поля допуска, то часто для характеристики вероятности указывают ширину поля допуска и отношение Δ / 2σ, называемое числом сигм. Иными словами, число сигм – это сколько значений σ укладывается в половине поля допуска. В нашем примере можно сказать, что точность автомата равна ±0,15 мм при 3 σ. Поскольку при одинаковом значении ppm поле допуска пропорционально σ, то зная ширину поля допуска для определенного числа сигм можно легко получить поле допуска для другого числа сигм. В таблице 1 приведены соответствия некоторых полей допуска при различном числе сигм.
Обратите внимание, что все эти рассуждения верны только при отсутствии систематической погрешности (µ = 0), т.е. для идеально откалиброванного автомата. В таблице 2 приведены значения вероятностей попадания случайной величины в допуск и выхода из него для наиболее широко используемых на практике стандартных диапазонов – от ±1σ до ±6σ.
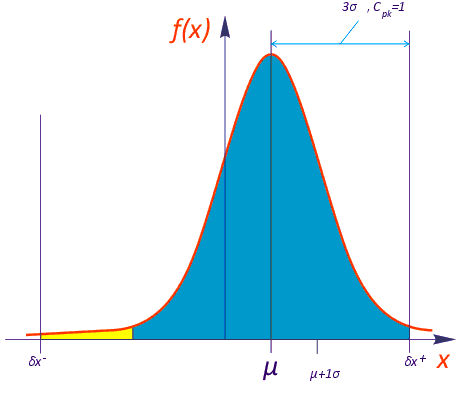
Очевидно, что диапазоны ±1σ и ±2σ не имеют реального практического значения для оценки точности из-за слишком большого числа компонентов, погрешность установки которых выходит за пределы этих диапазонов. Показатель воспроизводимости процесса сборки CpКак мы уже показали, для оценки принципиальной возможности автомата выполнить операцию сборки с заданной точностью достаточно определить поле допуска и число сигм. При этом автомат должен быть идеально откалиброван. Значения числа сигм менее 3 практического смысла не имеют. Поэтому иногда для оценки возможностей автомата в реальном производственном процессе пользуются показателем воспроизводимости процесса сборки Cp, который численно равен числу сигм, деленному на 3. Показатель Cp рассчитывается по следующей формуле:
Δx=δx+– δx– – поле допуска автомата; δx+; δx– – соответственно верхнее и нижнее отклонение поля допуска. Таким образом, для симметричного допуска (при δx+= δx–= δx):
Коэффициент Cp определяет принципиальную возможность исследуемого автомата обеспечивать качество установки компонентов, когда среднее значение ошибки установки лежит в середине поля допуска автомата, указанного в его технических характеристиках. Положение среднего и, следственно, систематические ошибки при этом не учитываются. Показатель реализуемости процесса СpkВсе время до этого мы говорили о случае, когда систематическая погрешность отсутствует, т.е. математическое ожидание µ = 0. На практике всегда существует определенная систематическая погрешность, связанная с точностью систем автомата. Более того, со временем автоматы склонны к раскалибровке, т.е. систематическая погрешность увеличивается. Если систематическая погрешность имеет достаточно большую величину, т.е. среднее положение компонентов достаточно близко к левой или правой границе поля допуска автомата, при сборке будет наблюдаться значительное число выходов ошибки за его пределы, хотя значение коэффициента Cp при этом может оставаться допустимым (см. рис. 4). Чтобы учесть положение математического ожидания (средней ошибки установки), вводится показатель реализуемости процесса Cpk.
Рис. 4. Показатели Cp и Cpk при значительной систематической погрешности. Показатель реализуемости процесса Cpk по определению равен:
Аналогично, в случае поля допуска, симметричного относительно µ:
Следует обратить внимание, что на практике в приложении к автоматам установки компонентов поле допуска как правило симметричное относительно нуля, а не µ. В этом случае последняя формула справедлива только при µ = 0, т.е. для идеально откалиброванного автомата, при этом Cpk = Cp.
Рис. 5. Показатель Cpk учитывает как случайную, так и систематическую погрешность Математический смысл показателя Cpk следующий: данный показатель равен числу σ, умещающихся между средним положением установленных компонентов (µ) и ближайшей к этому значению границе поля допуска, деленному на 3. Высокое значение показателя Cpk будет достигаться при значениях рассеивания ошибки σ, малых по сравнению с полем допуска автомата, и близком к нулю значении μ (рис. 5). Можно сказать, что использование данного показателя одновременно «сдвигает» на величину µ и «сужает» на величину 2µ поле допуска (см. рис. 6) по сравнению со случаем применения показателя Cp.
Рис. 6. Различные случаи, соответствующие одному значению Cpk.
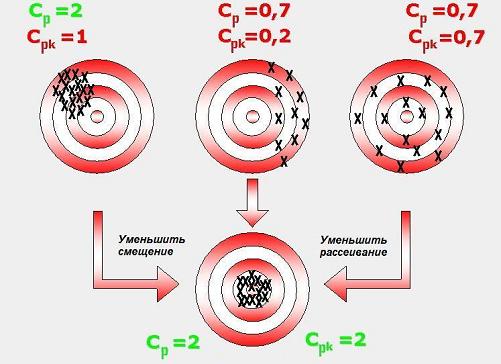
Рис. 7. Достижение высоких значений показателей Cp и Cpk возможно при одновременном снижении средней ошибки установки μ и ее рассеивания σ. Рисунок с сайта www.cetaq.net (с точностью до обозначений) Процесс теоретически считается воспроизводимым, если его Cp > 1,00. Тем не менее, воспроизводимый на практике процесс обладает показателем Cp > 1,33, так как необходимо заложить некоторый запас, связанный с возможным возникновением различных дополнительных погрешностей (раскалибровка автомата и пр.). Работоспособный процесс характеризуется значением Cpk > 1,33 [14]. Целевые значения показателей Cp и Cpk рассчитываются, исходя из определенных характеристик точности процесса/автомата на уровне ± N сигма. Ниже приведены соотношения, помогающие лучше понять связь между целевыми значениями и σ:
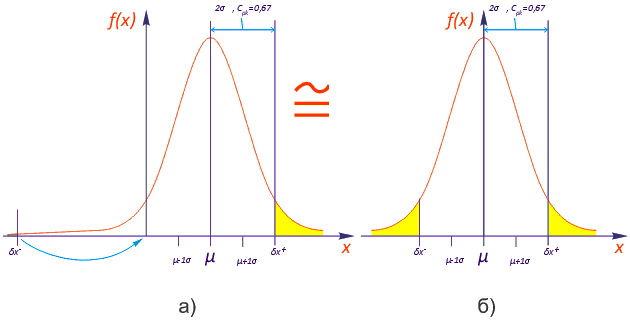
Если производитель автомата заявляет точность ±0,05 при Cpk = 1, это означает, что даже при µ ≠ 0 ppm будет не хуже 2700. Насколько при этом будет велико значение µ и σ пользователя волновать не должно: конструкцией автомата будет обеспечена заданная вероятность. Почему мы говорим «ppm будет не хуже», можно понять из графика на рис. 8. Поскольку данный показатель определяет число сигм, укладывающихся в расстояние между µ и «ближайшей» границей поля допуска, то в расстояние между µ и второй («дальней») границей будет укладываться большее число сигм, а значит общая вероятность правильной установки, например, при Cpk = 1 и µ ≠ 0 будет больше, чем вероятность из таблицы 1 для 3 σ (Cp = 1).
Рис. 8. Вероятность, неучитываемая показателем Cpk. Показатели Cm и CmkПоказатели Cp и Cpk используются не только при определении точности установки компонентов. Это универсальные показатели, используемые в инструментах систем качества для единого подхода в оценке повторяемости процессов. Как мы уже говорили, показатели точности процесса отличаются от показателей точности оборудования, поэтому вместо показателей Cp и Cpk, строго говоря, следует использовать показатели возможностей оборудования Cm и Cmk. Формулы для нахождения этих параметров идентичны приведенным выше для Cp и Cpk, различие заключается только в характере сбора статистической информации. На практике же обычно пользуются обозначениями Cp и Cpk и для показателей, характеризующих оборудование. Это не должно вводить в заблуждение, поэтому всегда нужно четко осознавать, о техпроцессе в целом, операции или оборудовании идет речь. Характеристики точности в спецификации автоматаПодведем небольшой итог в виде общего списка показателей точности, которые используются производителями автоматов при описании их технических характеристик. В данном списке под x будем понимать положение компонента по одной из координат x или y, либо углу поворота θ вокруг оси Z.
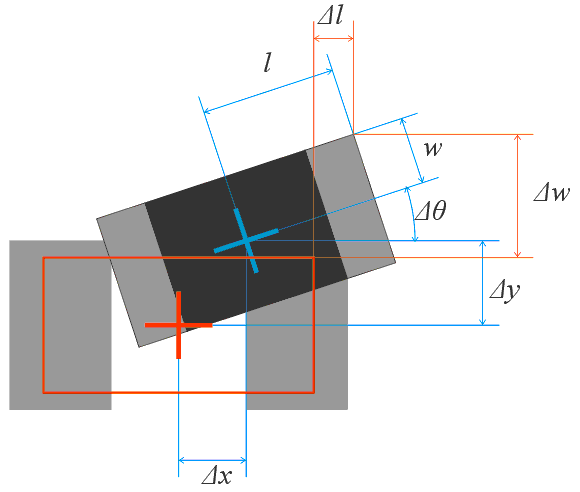
Точность установки разных типов корпусов: влияние трех степеней свободыПри установке компонента он имеет три степени свободы: по оси X, по оси Y и по углу поворота θ вокруг оси Z. Фактически, системой управления автомата обеспечивается точность положения центра масс компонента. Но на практике наиболее важным является совмещение вывода с контактной площадкой, однако зная точность положения центра масс, например, по оси X, мы не можем сказать, какова точность положения по оси X некоторой точки на выводе компонента, не зная точности по θ, а также геометрии компонента. Пусть компонент должен быть установлен в точку (x;y) в координатах платы; некоторая критичная точка A на выводе компонента имеет координаты относительно центра масс компонента (l;w); возможное отклонение положения центра масс компонента при заданной вероятности по трем степеням свободы равно, соответственно, Δx, Δy и Δθ. Тогда возможное отклонение положения точки A после установки при данной вероятности будет определяться следующими соотношениями:
Рис. 9. Результирующее смещение точки компонента Таким образом, погрешность установки центра масс может не отражать реального поля допуска установки компонента. Производитель, как правило, указывает только погрешность по одной оси. Как правило, погрешность автомата по второй оси равна либо меньше указанной. Однако, как учесть ошибку поворота компонента, если ее последствия связаны с конкретным типоразмером? Часто указанная в спецификации погрешность установки компонента справедлива для любой точки выводов (контактных поверхностей) определенного корпуса, т.е. учитывает погрешности по всем степеням свободы (в терминах приведенных выше формул производитель указывает не max{Δx, Δy} и Δθ, а max{Δl, Δw}). Этим типом корпуса может являться один из стандартных компонентов, указанных в стандарте IPC-9850 (чаще всего – ЧИП-компонент размера 0603), либо самый сложный корпус, установка которого гарантируется производителем автомата (например, QFP или BGA максимального размера с минимальным шагом выводов). Однако если производитель не ссылается на стандарт, по которому производилось измерение точности, и не указывает явно, какие компоненты устанавливаются с заданной точностью, эти вопросы следует уточнить. Что хотел сказать производитель?Рассмотрим три наиболее часто встречающихся варианта указания данных о точности автомата в его спецификации. 1. «Точность ±0,05 мм». Очевидно, что существует вероятность установки автоматом компонента вне поля допуска, однако, эту вероятность производитель не указал. Приведенная формулировка явно не полная. Иногда, если никаких сведений о вероятности нет, считается, что данное поле попуска приведено для 1 σ, но это не является общим правилом. В этом случае следует уточнить у производителя вероятностные характеристики точности. 2. «Точность ±0,05 мм при 3 σ». В данном случае производитель указал точность для идеально откалиброванного автомата. Небольшая раскалибровка будет причиной отклонения вероятностных показателей точности от указанных в спецификации, и к каким последствиям это приведет – не известно. Некоторые производители считают, что такая формулировка полностью идентична «точности ±0,05 мм при Cpk = 1», однако это также не является общим правилом. В этом случае у производителя следует уточнить, как на точность сборки будет влиять раскалибровка автомата. 3. «Точность ±0,05 мм при Cpk = 1». В данном случае производитель указал наиболее полную информацию о точности автомата, однако и здесь есть некоторая неоднозначность. Дело в том, что значение поля допуска при заданном Cpk, измеренное на только что откалиброванном автомате, будет отличаться от значения после некоторого времени работы из-за появления систематической погрешности. В этом случае стоит уточнить, в течение какого периода после калибровки производитель гарантирует данные характеристики. И в заключение первой части отметим еще одну особенность специфицируемых характеристик точности оборудования. Некоторые производители указывают, например, следующее: «Точность ±0,15 мм при 3 σ, ±0,20 мм при 4 σ». Зачем указывать два значения, если их можно пересчитать одно в другое (мы ранее показывали, что при µ = 0, число сигм пропорционально ширине поля допуска)? Дело в том, что в технических характеристиках оборудования приводят данные, подтвержденные при испытаниях. Например, данный автомат проходил испытания для 3 σ и 4 σ, но не проходил для 6 σ, и производитель не должен указывать в спецификации «Точность ±0,30 мм при 6 σ», хотя, скорее всего, это на практике будет верно. Как определяются параметры точности при испытаниях рассматривается во второй части. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© “Элинформ” 2007-2025. Информационный портал для производителей электроники: монтаж печатных плат, бессвинцовые технологии, поверхностный монтаж, производство электроники, автоматизация производства  |
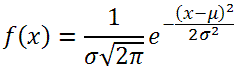
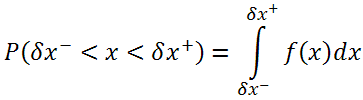
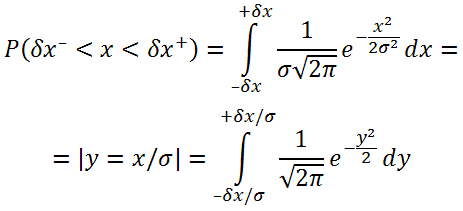
 , где
, где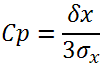 .
.
 , где
, где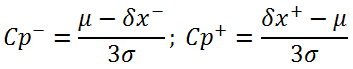
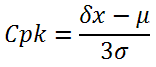 .
.